vanchinhdn215
Búa Gỗ
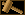
METRIC LÀ GÌ? có phải chỉ là một cái tên hoa mỹ cho tỉ lệ xích?, và tại sao nó lại gây cách mạng trong vật lí? tại sao máy bay không bay qua thái bình dương?
bạn sẽ hiểu ngay sau khi đọc hết bài này!
I Định nghĩa :
trước hết chúng ta cần phải bắt đầu về định nghĩa của từ "Metric".
"Metric là một thuật ngữ đo lường, thường được sử dụng rộng rãi cho những vấn đề liên quan đến sự đo lường, đơn vị hóa, vv.
để hiểu được vấn đề này, bạn hãy hình dung theo hai bước sau.
B1. Nhắm mắt lại, và tưởng tượng một mặt phẳng, có thể là một sân vân động, mặt phẳng tờ giấy, đại loại...
bây giờ vẽ một tam giác lên mặt phẳng này trong não bạn...bạn hình dung ra chưa, ok rất tốt!
giờ hãy vẽ ba góc lên tam giác này, và tính tổng của ba góc.
Chà, câu trả lời thật đơn giản, Tổng ba góc của một tam giác luôn là 180 độ, chẳng phải ai cũng đã học rồi sao, nhưng từ từ đã, chúng ta còn bước hai.
B2. giờ tiếp tục nhắm mắt lại, và liên tưởng đến một bề mặt, nhưng lần này là bề mặt cong.
hãy tưởng tượng đây là mặt cầu, có thể là bề mặt của một quả cam, trái banh,hay tốt hơn, là hãy hình dung trái đất của chúng ta.
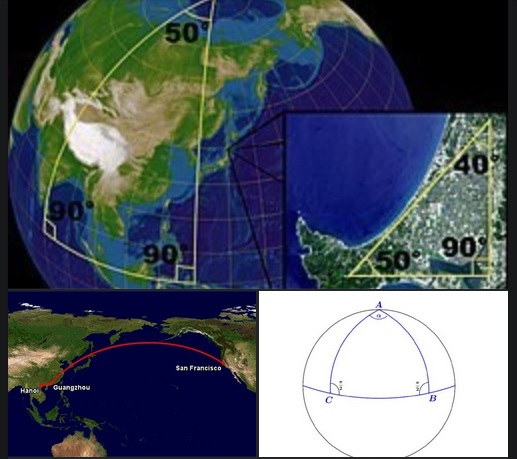
bây giờ hãy đi 10,000 km trên bề mặt của trái đất, sau đó rẽ 90 độ vuông góc với đường đi của bạn và đi thêm 10,000 km nữa, sau đó lại rẽ 90 độ vuông góc với đường bạn vừa đi, bạn sẽ về lại điểm xuất phát trên bề mặt.
Chà, bạn vừa vẽ một tam giác trên bề mặt của trái đất đấy, với ba góc vuông 90 độ chẳng.
nếu bạn chưa hình dung ra thì hãy xem ảnh minh họa mình để bên dưới.
bạn có nhớ những gì mình đã làm trong bước 1 hay không?
Vâng, bạn đã vẽ một tam giác, với tổng các góc = 180 độ.
nhưng khoang đã, có phải tôi vừa nói rẽ vuông góc 90 độ ba lần trên mặt cầu để có một tam giác hoàn chỉnh không.
Vâng!...cái gì, đợi đã, không thể nào, (90 độ) * (3 lần) = 270 độ, không thể nào! một tam giác không thể có tổng các góc > 180 độ, đây không phải là một tam giác!
Chà...khoan hãy vội kết luận.
Đúng vậy!, giờ chúng ta có hai sự lựa chọn.
Một...là cái tam giác bạn vừa vẽ trên bề mặt cầu không thực sự là một tam giác, vì tam giác luôn cộng lại = 180 độ.
song thì lại kỳ lạ, vì tam giác nghĩa là có ba cạnh, và tam giác trên mặt cầu thỏa mãn điều kiện trên.
Hai...là cái quy luật Tổng = 180 độ của tam giác chỉ áp dụng được trong trường hợp đặc biệt của hình học, tức là "hình học Euclid", hay hình học bình thường.
nhưng trước khi có câu trả lời cho câu hỏi hóc búa này, hãy sang ví dụ tiếp theo bạn nhé.
II : Metric nghĩa là input khoảng cách giả và output khoảng cách thực :
bây giờ thử viết phương trình tổng các góc trên mặt cầu, và thử nhân nó cho một hằng số, hãy gọi là "k".
ta có một công thức là "(A+B+C)*k" , và "k" được điều chỉnh thích hợp để cho tổng của phép tính luôn bằng 180 độ, vì vậy bạn có thể quay lại hình học bình thường.
nếu (A+B+C)k = 180 độ thì k có giá trị = 1, chứng tỏ bề mặt này phẳng.
k trên mặt cầu sẽ có giá trị là chính xác là 157/(50π) hay 0.9994 đơn vị.
hóa ra hằng số "k" này thực sự liên quan đến độ cong của bề mặt mà ta đang miêu tả, hóa ra nếu bề mặt càng cong, thì "k" sẽ càng nhỏ đi, và ta có thể lấy nghịch đảo của hằng số "k" để có một thước đo tương đối về độ cong của một bề mặt, sẽ là một ý tưởng rất hay.
tuy nhiên, giờ hãy tạm gác phép tính này qua một bên, và nhớ lại bản đồ của trái đất mà bạn thường hay thấy trên google map.
Vâng, bản đồ đó thực sự trông phẳng, nhưng nó có thực sự phẳng hay không? vì ta biết trái đất thực chất là hình cầu.
Bạn hãy hình dung như sau, sau đó đặt câu hỏi cho bản thân.
1. trong bản đồ in phẳng ta hay thấy, hai địa điểm nối nhau (Hà nội,San Francisco) vẽ một đường thẳng cắt ngang qua biển thái bình dương.
giờ hãy vào google map, nhấp chuột phải vào Hà Nội, sau đó chọn đo khoảng cách, và kéo chuột đến San Francisco, bạn sẽ nhận thấy, đường vẽ ra trên bản đồ bị cong,
(nếu bạn không làm được thì vui lòng xem hình bên dưới bài viết).
nhưng kỳ lạ thay, đó lại là đường ngắn nhất? Đúng thế!
vì metric trên bản đồ là vô thường, hay nói cách khác k ≠ 1 .
trên metric này con đường quẹo cong từ Hà Nội đến San Francisco khoảng cách "ngắn nhất",
còn đường thẳng đi qua thái bình dương trên bản đồ in phẳng thực chất là một đường dài hơn.
hóa ra, bề mặt của trái đất, cái hình học đang tồn tại trong thực tế, gọi là "Đa Tạp".
còn hình vẽ của nó trên bản đồ được gọi là "Hệ Tọa độ" (Coordinate system).
hóa ra, hệ tọa độ là một sự lựa chọn tùy ý, bạn có thể chọn một hệ tọa độ mà trái đất trong có hình donut, thay vì hình phẳng, và tọa độ khác để thấy trái đất hình trụ cũng được.
nhưng hóa ra, hệ tọa độ mà bạn chọn không hề ảnh hưởng đến đa tạp (thực tế), phép đo của bạn trên tọa độ luôn phải tích với một cái gì đó để đổi ra phép đo thực.
đây là cái mà chúng ta thường gọi là tỉ lệ xích.
ví dụ tỉ lệ xích là 1 triệu, nghĩa là 1 cm trên bản đồ là 10 km ngoài đời thực.
bạn thấy không? ta input dữ liệu ảo và output dữ liệu thực.
và đây chính xác là ý nghĩa của Metric.
cho dữ liệu ảo vào và rút ra dữ liệu thật.
III : Tensor metric (gμν) .
bạn còn nhớ định lý Pytago chứ?
a²+b² = c² , vâng , là nó!
hãy vi phân hóa định lý Pytago, tức là thay vì ta có một tam giác vuông có diện tích ≠ 0, ta có một tam giác vuông với diện tích -> 0.
ta có công thức như sau :
ds² = dx² + dy², và "ds" đại diện cho khoảng cách vô cùng nhỏ giữa hai điểm trên tọa độ.
ghi dưới dạng tổng của vector ta có : ds = (dxεˣ + dyεʸ)
ε đại diện cho vector cơ sở của tọa độ.
sử dụng tích vô hướng "." ta có :
ds² = ds . ds = (dxεˣ + dyεʸ) . (dxεˣ + dyεʸ)
= (dx dx)(εˣ.εˣ) + (dx dy) (εˣ.εʸ) + dy dx(εʸ.εˣ) + (dy dy)(εʸ.εʸ)
hóa ra định lý Pytago là một trường hợp đặt biệt, khi hệ tọa độ của bạn là bình thường, tức là tọa độ phẳng trên mặt phẳng.
trong trường hợp này
tích vô hướng của hai vector cơ sở có cùng thành phần, ví dụ như
"εˣ.εˣ" hay εʸ.εʸ , có giá trị = 1 .
còn tích của hai vector cơ sở có giá trị ≠ 1 ví dụ như
εˣ.εʸ , hay εʸ.εˣ = 0 .
hóa ra trong tọa độ (Euclid), tức là mặt phẳng,
ta có tích vector cơ sở như sau :
εˣ. εˣ = 1
εˣ. εʸ = 0
εʸ. εˣ = 0
εʸ. εʸ = 1
nếu tọa độ của bạn là cong trên mặt phẳng, hay mặt cong được đo bởi một loại tọa độ mà nó trong phẳng, thì định lý Pytago không còn áp dụng được nữa,
cũng như định luật Tổng ba góc = 180 độ không thể áp dụng khi bề mặt chứa độ cong 1/k.
trên mặt cầu, cách để tính khoảng cách giữa hai điểm là
ds² = R² dθ²+ R²cos²(θ) dϕ² .
R đại diện cho bán kính của mặt cầu
θ đại diện cho tọa độ kinh tuyến
ϕ đại diện cho tọa độ vĩ tuyến.
còn (R²,R²cos²(θ), giống như hằng số k đó, chỉ ở đó để cho ouput của phép toán ra khoảng cách thực tế.
vâng, ta có thể lập ra một ma trận để miêu tả các thành phần này.
ma trận này hóa ra là một tensor, được gọi là tensor metric (gμν).
gμν là một tensor hạng 2 có 4 thành phần là (g00, g01, g10, g11).
hóa ra ở tọa độ mặt cầu,
g00 = ε⁰. ε⁰ = R²
g01 = ε⁰. ε¹ = 0
g10 = ε¹. ε⁰ = 0
g11 = ε¹. ε¹ = R²cos²(θ).
và công thức toán học để tính khoảng cách là ds²= g00 dx0 dx0 + g01 dx0 dx1 + g10 dx1 dx0 +g11 dx1 dx1 .
trên mặt cầu ta đổi ký hiệu đơn vị, dx0 -> dθ, còn dx1 -> dϕ
ta có tổng biểu thức của ds² = R² dθdθ + 0 dθdϕ + 0dϕdθ + R²cos²(θ) dϕdϕ.
rút gọn thành ds² = R² dθ²+ R²cos²(θ) dϕ².
và trên tọa độ Euclid bình thường, tức mặt phẳng,
g00 = 1
g01 = 0
g10 = 0
g11 = 1
và phương trình trở thành ds² = 1 dx0 dx0 + 0 dx0dx1 + 0 dx1dx0
+ 1 dx1dx1 = (dx0)²+(dx1)² , do đó ta trở về định lý Pytago.
IV : Kết Luận Và Bài Học Rút Ra :
hóa ra, kinh tuyến và vĩ tuyến đều là phép đo giả, nhưng nhờ Tensor metric, cho ta biết khoảng cách thực sự giữa hai điểm trên mặt cầu.
trên mặt cầu, ta thấy kinh tuyến và vĩ tuyến không hề thẳng vuông góc với nhau như hai trục trên tọa độ bình thường, nhưng bạn có thể bóp phẳng nó và kết quả thu được là bản đồ in phẳng của mặt cầu đó, y hệt như của trái đất.
và đường thẳng trên đa tạp như chuyến bay từ Hà Nội đến San fansico , sẽ trông như bị cong khi ta vẽ trên một tọa độ kinh tuyến vĩ tuyến, và làm phẳng chúng.
V : Ứng Dụng Thực Tế :
khái niệm Tensor metric và hình học vi phân đã trở thành phương pháp cơ sở cho việc xây dựng thuyết tương đối rộng của Einstein, lý thuyết miêu tả lực hấp dẫn chính xác nhất của nhân loại hiện nay được chứng minh bởi thực nghiệm.
mình cũng đã làm về một bài nói về lực hấp dẫn và thực chất nó là một ảo ảnh do hai đường thẳng song song gặp nhau trên mặt cong được xuất bản vào 29/5/2021, bạn có thể xem trong hồ sơ của mình tại group.
VI : Lưu ý trước khi kết bài.
công thức (A+B+C)k = 180 độ hoàn toàn do mình làm nên, và không phải là cách chính xác nhất để tính ra độ cong thực sự của bề mặt.
đó chỉ là một mô hình mình tạo dựng để cho các bạn nắm được ý tưởng toán học đằng sau hình học vi phân mà thôi, nên các bạn đừng tiếp thu phương trình này của mình một cách nghiêm túc nhé.
cách để tính độ cong của một bề mặt là sử dụng Tensor Riemann, nhưng do quá phức tạp nên có lẽ mình sẽ để dành nó cho chủ đề sau,
nhưng phương trình ds² = R² dθ²+ R²cos²(θ) dϕ² là hoàn toàn có thật và metric là tọa độ mặt cầu nhé.
mục đích của bài viết là cho bạn hiểu về mục đích chủ đạo của lý thuyết, còn nếu bạn muốn đào sâu vào phần toán học của hình học này, bạn có thể tham khảo từ khóa như sau : "hình học vi phân", "giải tích tensor" , "đa tạp".
bạn có thể tìm những quyển sách có chủ đề tương tự và tự nghiên cứu chúng.
chúc các bạn thành công!
Kết Bài : hy vọng bạn sẽ có cái nhìn khác về hình học sau khi đọc và ngẫm bài viết này, từ một câu hỏi đơn giản, dẫn đến lý thuyết cách mạng nhất của nhân loại?
hãy chia sẽ cảm nghĩ của bạn!
Nguồn Fb quach minh dang
bạn sẽ hiểu ngay sau khi đọc hết bài này!

trước hết chúng ta cần phải bắt đầu về định nghĩa của từ "Metric".
"Metric là một thuật ngữ đo lường, thường được sử dụng rộng rãi cho những vấn đề liên quan đến sự đo lường, đơn vị hóa, vv.
để hiểu được vấn đề này, bạn hãy hình dung theo hai bước sau.
B1. Nhắm mắt lại, và tưởng tượng một mặt phẳng, có thể là một sân vân động, mặt phẳng tờ giấy, đại loại...
bây giờ vẽ một tam giác lên mặt phẳng này trong não bạn...bạn hình dung ra chưa, ok rất tốt!
giờ hãy vẽ ba góc lên tam giác này, và tính tổng của ba góc.
Chà, câu trả lời thật đơn giản, Tổng ba góc của một tam giác luôn là 180 độ, chẳng phải ai cũng đã học rồi sao, nhưng từ từ đã, chúng ta còn bước hai.
B2. giờ tiếp tục nhắm mắt lại, và liên tưởng đến một bề mặt, nhưng lần này là bề mặt cong.
hãy tưởng tượng đây là mặt cầu, có thể là bề mặt của một quả cam, trái banh,hay tốt hơn, là hãy hình dung trái đất của chúng ta.
bây giờ hãy đi 10,000 km trên bề mặt của trái đất, sau đó rẽ 90 độ vuông góc với đường đi của bạn và đi thêm 10,000 km nữa, sau đó lại rẽ 90 độ vuông góc với đường bạn vừa đi, bạn sẽ về lại điểm xuất phát trên bề mặt.
Chà, bạn vừa vẽ một tam giác trên bề mặt của trái đất đấy, với ba góc vuông 90 độ chẳng.
nếu bạn chưa hình dung ra thì hãy xem ảnh minh họa mình để bên dưới.
bạn có nhớ những gì mình đã làm trong bước 1 hay không?
Vâng, bạn đã vẽ một tam giác, với tổng các góc = 180 độ.
nhưng khoang đã, có phải tôi vừa nói rẽ vuông góc 90 độ ba lần trên mặt cầu để có một tam giác hoàn chỉnh không.
Vâng!...cái gì, đợi đã, không thể nào, (90 độ) * (3 lần) = 270 độ, không thể nào! một tam giác không thể có tổng các góc > 180 độ, đây không phải là một tam giác!
Chà...khoan hãy vội kết luận.
Đúng vậy!, giờ chúng ta có hai sự lựa chọn.
Một...là cái tam giác bạn vừa vẽ trên bề mặt cầu không thực sự là một tam giác, vì tam giác luôn cộng lại = 180 độ.
song thì lại kỳ lạ, vì tam giác nghĩa là có ba cạnh, và tam giác trên mặt cầu thỏa mãn điều kiện trên.
Hai...là cái quy luật Tổng = 180 độ của tam giác chỉ áp dụng được trong trường hợp đặc biệt của hình học, tức là "hình học Euclid", hay hình học bình thường.
nhưng trước khi có câu trả lời cho câu hỏi hóc búa này, hãy sang ví dụ tiếp theo bạn nhé.
II : Metric nghĩa là input khoảng cách giả và output khoảng cách thực :
bây giờ thử viết phương trình tổng các góc trên mặt cầu, và thử nhân nó cho một hằng số, hãy gọi là "k".
ta có một công thức là "(A+B+C)*k" , và "k" được điều chỉnh thích hợp để cho tổng của phép tính luôn bằng 180 độ, vì vậy bạn có thể quay lại hình học bình thường.
nếu (A+B+C)k = 180 độ thì k có giá trị = 1, chứng tỏ bề mặt này phẳng.
k trên mặt cầu sẽ có giá trị là chính xác là 157/(50π) hay 0.9994 đơn vị.
hóa ra hằng số "k" này thực sự liên quan đến độ cong của bề mặt mà ta đang miêu tả, hóa ra nếu bề mặt càng cong, thì "k" sẽ càng nhỏ đi, và ta có thể lấy nghịch đảo của hằng số "k" để có một thước đo tương đối về độ cong của một bề mặt, sẽ là một ý tưởng rất hay.
tuy nhiên, giờ hãy tạm gác phép tính này qua một bên, và nhớ lại bản đồ của trái đất mà bạn thường hay thấy trên google map.
Vâng, bản đồ đó thực sự trông phẳng, nhưng nó có thực sự phẳng hay không? vì ta biết trái đất thực chất là hình cầu.
Bạn hãy hình dung như sau, sau đó đặt câu hỏi cho bản thân.
1. trong bản đồ in phẳng ta hay thấy, hai địa điểm nối nhau (Hà nội,San Francisco) vẽ một đường thẳng cắt ngang qua biển thái bình dương.
giờ hãy vào google map, nhấp chuột phải vào Hà Nội, sau đó chọn đo khoảng cách, và kéo chuột đến San Francisco, bạn sẽ nhận thấy, đường vẽ ra trên bản đồ bị cong,
(nếu bạn không làm được thì vui lòng xem hình bên dưới bài viết).
nhưng kỳ lạ thay, đó lại là đường ngắn nhất? Đúng thế!
vì metric trên bản đồ là vô thường, hay nói cách khác k ≠ 1 .
trên metric này con đường quẹo cong từ Hà Nội đến San Francisco khoảng cách "ngắn nhất",
còn đường thẳng đi qua thái bình dương trên bản đồ in phẳng thực chất là một đường dài hơn.
hóa ra, bề mặt của trái đất, cái hình học đang tồn tại trong thực tế, gọi là "Đa Tạp".
còn hình vẽ của nó trên bản đồ được gọi là "Hệ Tọa độ" (Coordinate system).
hóa ra, hệ tọa độ là một sự lựa chọn tùy ý, bạn có thể chọn một hệ tọa độ mà trái đất trong có hình donut, thay vì hình phẳng, và tọa độ khác để thấy trái đất hình trụ cũng được.
nhưng hóa ra, hệ tọa độ mà bạn chọn không hề ảnh hưởng đến đa tạp (thực tế), phép đo của bạn trên tọa độ luôn phải tích với một cái gì đó để đổi ra phép đo thực.
đây là cái mà chúng ta thường gọi là tỉ lệ xích.
ví dụ tỉ lệ xích là 1 triệu, nghĩa là 1 cm trên bản đồ là 10 km ngoài đời thực.
bạn thấy không? ta input dữ liệu ảo và output dữ liệu thực.
và đây chính xác là ý nghĩa của Metric.
cho dữ liệu ảo vào và rút ra dữ liệu thật.
III : Tensor metric (gμν) .
bạn còn nhớ định lý Pytago chứ?
a²+b² = c² , vâng , là nó!
hãy vi phân hóa định lý Pytago, tức là thay vì ta có một tam giác vuông có diện tích ≠ 0, ta có một tam giác vuông với diện tích -> 0.
ta có công thức như sau :
ds² = dx² + dy², và "ds" đại diện cho khoảng cách vô cùng nhỏ giữa hai điểm trên tọa độ.
ghi dưới dạng tổng của vector ta có : ds = (dxεˣ + dyεʸ)
ε đại diện cho vector cơ sở của tọa độ.
sử dụng tích vô hướng "." ta có :
ds² = ds . ds = (dxεˣ + dyεʸ) . (dxεˣ + dyεʸ)
= (dx dx)(εˣ.εˣ) + (dx dy) (εˣ.εʸ) + dy dx(εʸ.εˣ) + (dy dy)(εʸ.εʸ)
hóa ra định lý Pytago là một trường hợp đặt biệt, khi hệ tọa độ của bạn là bình thường, tức là tọa độ phẳng trên mặt phẳng.
trong trường hợp này
tích vô hướng của hai vector cơ sở có cùng thành phần, ví dụ như
"εˣ.εˣ" hay εʸ.εʸ , có giá trị = 1 .
còn tích của hai vector cơ sở có giá trị ≠ 1 ví dụ như
εˣ.εʸ , hay εʸ.εˣ = 0 .
hóa ra trong tọa độ (Euclid), tức là mặt phẳng,
ta có tích vector cơ sở như sau :
εˣ. εˣ = 1
εˣ. εʸ = 0
εʸ. εˣ = 0
εʸ. εʸ = 1
nếu tọa độ của bạn là cong trên mặt phẳng, hay mặt cong được đo bởi một loại tọa độ mà nó trong phẳng, thì định lý Pytago không còn áp dụng được nữa,
cũng như định luật Tổng ba góc = 180 độ không thể áp dụng khi bề mặt chứa độ cong 1/k.
trên mặt cầu, cách để tính khoảng cách giữa hai điểm là
ds² = R² dθ²+ R²cos²(θ) dϕ² .
R đại diện cho bán kính của mặt cầu
θ đại diện cho tọa độ kinh tuyến
ϕ đại diện cho tọa độ vĩ tuyến.
còn (R²,R²cos²(θ), giống như hằng số k đó, chỉ ở đó để cho ouput của phép toán ra khoảng cách thực tế.
vâng, ta có thể lập ra một ma trận để miêu tả các thành phần này.
ma trận này hóa ra là một tensor, được gọi là tensor metric (gμν).
gμν là một tensor hạng 2 có 4 thành phần là (g00, g01, g10, g11).
hóa ra ở tọa độ mặt cầu,
g00 = ε⁰. ε⁰ = R²
g01 = ε⁰. ε¹ = 0
g10 = ε¹. ε⁰ = 0
g11 = ε¹. ε¹ = R²cos²(θ).
và công thức toán học để tính khoảng cách là ds²= g00 dx0 dx0 + g01 dx0 dx1 + g10 dx1 dx0 +g11 dx1 dx1 .
trên mặt cầu ta đổi ký hiệu đơn vị, dx0 -> dθ, còn dx1 -> dϕ
ta có tổng biểu thức của ds² = R² dθdθ + 0 dθdϕ + 0dϕdθ + R²cos²(θ) dϕdϕ.
rút gọn thành ds² = R² dθ²+ R²cos²(θ) dϕ².
và trên tọa độ Euclid bình thường, tức mặt phẳng,
g00 = 1
g01 = 0
g10 = 0
g11 = 1
và phương trình trở thành ds² = 1 dx0 dx0 + 0 dx0dx1 + 0 dx1dx0
+ 1 dx1dx1 = (dx0)²+(dx1)² , do đó ta trở về định lý Pytago.
IV : Kết Luận Và Bài Học Rút Ra :
hóa ra, kinh tuyến và vĩ tuyến đều là phép đo giả, nhưng nhờ Tensor metric, cho ta biết khoảng cách thực sự giữa hai điểm trên mặt cầu.
trên mặt cầu, ta thấy kinh tuyến và vĩ tuyến không hề thẳng vuông góc với nhau như hai trục trên tọa độ bình thường, nhưng bạn có thể bóp phẳng nó và kết quả thu được là bản đồ in phẳng của mặt cầu đó, y hệt như của trái đất.
và đường thẳng trên đa tạp như chuyến bay từ Hà Nội đến San fansico , sẽ trông như bị cong khi ta vẽ trên một tọa độ kinh tuyến vĩ tuyến, và làm phẳng chúng.
V : Ứng Dụng Thực Tế :
khái niệm Tensor metric và hình học vi phân đã trở thành phương pháp cơ sở cho việc xây dựng thuyết tương đối rộng của Einstein, lý thuyết miêu tả lực hấp dẫn chính xác nhất của nhân loại hiện nay được chứng minh bởi thực nghiệm.
mình cũng đã làm về một bài nói về lực hấp dẫn và thực chất nó là một ảo ảnh do hai đường thẳng song song gặp nhau trên mặt cong được xuất bản vào 29/5/2021, bạn có thể xem trong hồ sơ của mình tại group.
VI : Lưu ý trước khi kết bài.
công thức (A+B+C)k = 180 độ hoàn toàn do mình làm nên, và không phải là cách chính xác nhất để tính ra độ cong thực sự của bề mặt.
đó chỉ là một mô hình mình tạo dựng để cho các bạn nắm được ý tưởng toán học đằng sau hình học vi phân mà thôi, nên các bạn đừng tiếp thu phương trình này của mình một cách nghiêm túc nhé.
cách để tính độ cong của một bề mặt là sử dụng Tensor Riemann, nhưng do quá phức tạp nên có lẽ mình sẽ để dành nó cho chủ đề sau,
nhưng phương trình ds² = R² dθ²+ R²cos²(θ) dϕ² là hoàn toàn có thật và metric là tọa độ mặt cầu nhé.
mục đích của bài viết là cho bạn hiểu về mục đích chủ đạo của lý thuyết, còn nếu bạn muốn đào sâu vào phần toán học của hình học này, bạn có thể tham khảo từ khóa như sau : "hình học vi phân", "giải tích tensor" , "đa tạp".
bạn có thể tìm những quyển sách có chủ đề tương tự và tự nghiên cứu chúng.
chúc các bạn thành công!
Kết Bài : hy vọng bạn sẽ có cái nhìn khác về hình học sau khi đọc và ngẫm bài viết này, từ một câu hỏi đơn giản, dẫn đến lý thuyết cách mạng nhất của nhân loại?
hãy chia sẽ cảm nghĩ của bạn!
Nguồn Fb quach minh dang

