Vn-Z.vn Ngày 11 tháng 11 năm 2022, Mặt trời rất nóng , đó là sự thật mà tất cả mọi người trên trái đất đều biết. Thông thường để đo nhiệt độ các đồ vật người ta dùng nhiệt kế . Nhưng với "thứ" nóng như Mặt trời thì làm cách nào /?
Nhiệt độ bề mặt của Mặt Trời vào khoảng 5.537 độ C, trong khi đó nhiệt độ bên trong lõi của Mặt Trời lên đến khoảng 15 triệu độ C.

Rất Nhiều nhà thiên văn muốn biết nhiệt độ của mặt trời, một trong những nguồn động lực ban đầu để xác định hằng số mặt trời là tính nhiệt độ của mặt trời. Hằng số mặt trời là lượng năng lượng tiếp xúc với đỉnh bầu khí quyển của Trái đất, tính bằng watt trên mét bình phương. Điều này bao gồm năng lượng tích tụ từ toàn bộ phổ bức xạ mặt trời: vô tuyến, hồng ngoại, ánh sáng nhìn thấy, tia cực tím và tia X. Giá trị gần đúng của hằng số là 1,361 W /m bình phương. Thật đáng tiếc là mặc dù hằng số mặt trời đo được trong những ngày đầu và độ sáng mặt trời được tính từ nó không xa giá trị hiện đại (ít nhất là theo cùng một thứ tự độ lớn), cơ sở lý thuyết để liên kết chúng với nhiệt độ mặt trời đã bị bỏ qua . Lúc này xuất hiện nhiều lý thuyết để đo nhiệt độ Mặt trời khiến chúng khá hỗn loạn.
Có nhiều phương pháp khác nhau để ước tính nhiệt độ mặt trời , từ "tia nhiệt" không tồn tại đến Định luật làm mát Newton . Theo như kết quả tính toán, Mặt trời sẽ có thể đo từ hơn 1.000 độ đến vài triệu độ. ?
Để khuyến khích những nghiên cứu đáng tin cậy và chính xác, năm 1876, Viện Hàn lâm Khoa học Paris ở Pháp đã đặc biệt thiết lập một giải thưởng về tính toán nhiệt độ của mặt trời, nhưng rất tiếc là phương pháp này chưa thật chính xác. Dù giải thưởng đã được trao cho nhà vật lý người Pháp Jules Violle (1841 -1923). Nhưng phương pháp của ông thu được kết quả bằng phép tính rất "không đáng tin cậy" Mặt trời có nhiệt độ ở 1500-2500 ° C.

Joseph Stefan nhà vật lý, toán học, và nhà thơ gốc Slovenia của Đế quốc Áo
Cơ sở lý thuyết để tính nhiệt độ của mặt trời đã được nhà vật lý người Áo Joseph Stefan (Joseph Stefan, 1835-1893) đưa ra từ năm 1879 và 1884 từ dữ liệu thực nghiệm, và sau đó là đồng hương của ông là Ludwig Boltzmann (Ludwig Boltzmann, 1893) năm 1844. -1906) tiếp tục thực hiện các nghiên cứu có nguồn gốc từ nhiệt động lực học.

Ludwig Boltzmann
Hai nhà khoa học phát hiện ra rằng công suất bức xạ trên một đơn vị diện tích của vật đen (nghĩa là năng lượng bức xạ trong một giây) tỷ lệ với nhiệt độ tuyệt đối được nâng lên lũy thừa thứ tư. Định luật này ngày nay được gọi là định luật Stefan-Boltzmann, và hệ số tỷ lệ được gọi là hằng số Stefan-Boltzmann. Trong Hệ đơn vị Quốc tế, giá trị của hằng số Stefan-Boltzmann là
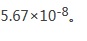
Mặc dù định luật Stefan-Boltzmann nhằm vào vật đen, nhưng hầu hết bức xạ sao tương đối gần với bức xạ vật đen, vì vậy định luật này cũng có thể áp dụng gần đúng cho bức xạ sao. Với định luật này, có một cơ sở lý thuyết để tính toán nhiệt độ bề mặt của mặt trời.
Phương pháp tính toán rất đơn giản: (theo thang nhiệt độ tuyệt đối) lũy thừa thứ tư của nhiệt độ bề mặt nhân với hằng số Stefan-Boltzmann là công suất bức xạ trên một mét vuông bề mặt của mặt trời, sau đó nhân với diện tích bề mặt của Mặt trời, nó là tổng bức xạ của mặt trời Công suất (nghĩa là tổng năng lượng bức xạ trong một giây), là độ chói của mặt trời của chúng ta.
Với phương pháp trên, Không khó để có được - nhiệt độ bề mặt của mặt trời (chính xác là nhiệt độ hiệu dụng của quang quyển ) vào khoảng 5800K (K là đơn vị nhiệt độ của thang nhiệt độ tuyệt đối, và 0 ° C trên thang độ C là khoảng 273K).
Ngoài phương pháp trên, các nhà khoa học còn có phương pháp nào ?
Trong phép tính trên, ngoài việc sử dụng định luật Stefan-Boltzmann, còn cần biết giá trị của hằng số Stefan-Boltzmann và độ chói của mặt trời. Nhưng trên thực tế, miễn là có mối quan hệ lũy thừa thứ tư được đưa ra bởi định luật Stefan-Boltzmann, ngay cả khi chúng ta không biết độ lớn của hằng số Stefan-Boltzmann, hoặc thậm chí độ chói của mặt trời, chúng ta vẫn có thể tính được nhiệt độ bề mặt của mặt trời.
Phương pháp này cũng rất đơn giản: chúng ta biết rằng nhiệt độ trung bình của bề mặt trái đất là khoảng 290K (tức là 17 ° C - đây là mức trung bình kép của vị trí và thời gian), nhưng một hành tinh có nhiệt độ như vậy cũng bức xạ năng lượng hướng ra bên ngoài, và năng lượng này cũng có thể được mô tả gần đúng bằng định luật Stefan-Boltzmann.
Vì không thể tự phát ra ánh sáng như mặt trời nên năng lượng trên bề mặt Trái đất chủ yếu đến từ ánh sáng mặt trời. Ngoài ánh sáng mặt trời, năng lượng nhận được trên bề mặt trái đất còn có sự đóng góp của bên trong trái đất. Tuy nhiên, công suất trung bình của cái sau chỉ là 0,06 W / m2, nhỏ hơn 1 / 10.000 năng lượng của ánh sáng mặt trời và có thể bị bỏ qua trong tính toán bằng phương pháp này.
Trái đất có thể duy trì nhiệt độ bề mặt hiện tại, có nghĩa là năng lượng mà nó tỏa ra về cơ bản bằng với năng lượng mà nó nhận được từ ánh sáng mặt trời. Sử dụng mối quan hệ này, chúng ta có thể tính toán nhiệt độ bề mặt của mặt trời.
Bạn thấy hằng số Stefan-Boltzmann sẽ tự động bị loại bỏ trong quá trình tính toán, và kết quả tính được là khoảng 6000K, tuy không chính xác như phương pháp trước nhưng cũng không khác nhiều.
Điều thú vị của phương pháp này là sử dụng nhiệt độ của hành tinh để suy ra nhiệt độ của ngôi sao. Nhưng điều thú vị hơn là, chúng ta cũng có thể suy ra nhiệt độ của các hành tinh ở một khoảng cách nhất định so với nhiệt độ của ngôi sao. Phương pháp này thường được các nhà thiên văn học sử dụng để ước tính vị trí và chiều rộng của vùng có thể sinh sống xung quanh một ngôi sao có khả năng tồn tại sự sống.
Tất nhiên, phương pháp tính toán này có những hạn chế lớn, ví dụ, nó đòi hỏi sự tồn tại của những thứ như nước và khí quyển trên hành tinh có thể làm cho nhiệt độ đồng nhất, và cũng yêu cầu bầu khí quyển không chứa nhiều khí gây hiệu ứng nhà kính ví dụ như khí quyển của sao Kim.
Ngay sau khi định luật Stefan-Boltzmann ra đời, nhà vật lý người Đức Wilhelm Wien (1864-1928) đã sử dụng nhiệt động lực học để chứng minh một định luật gọi là định luật chuyển vị Wien. (Wien‘s displacement law)

Wilhelm Carl Werner Otto Fritz Franz Wien
Định luật này cho thấy rằng nhiệt độ bề mặt của vật thể càng cao thì sự phân bố quang phổ càng bị dịch chuyển theo hướng sóng ngắn và màu sắc bị chuyển sang hướng xanh lam.
Áp dụng định luật này, các nhà thiên văn học đã phân loại các ngôi sao thành bảy loại theo đặc điểm quang phổ của chúng, được ký hiệu lần lượt là O, B, A, F, G, K và M.

Trong số đó, các thiên thể loại O có màu xanh lam, với nhiệt độ bề mặt cao nhất, trên 33000K, các thiên thể loại M có màu đỏ, với nhiệt độ bề mặt thấp nhất, dưới 3700K.
Các thiên thể màu vàng như mặt trời thuộc loại G và có nhiệt độ bề mặt từ 5200 đến 6000K. Trong mười loại phụ được chia theo thứ tự nhiệt độ từ cao đến thấp, được biểu thị bằng các chữ số Ả Rập từ 0 đến 9, 0 có nghĩa là nhiệt độ cao nhất và 9 có nghĩa là nhiệt độ thấp nhất.
Loại quang phổ của mặt trời là G2, được coi là loại có nhiệt độ cao hơn trong số loại G. Trong một số tài liệu, quang phổ của mặt trời được đánh dấu là G2V, khiến nó có màu trắng, và thường có màu vàng khi nhìn từ bề mặt Trái Đất bởi sự tán xạ khí quyển . Trong đó "V" không phải là chữ cái tiếng Anh "V", mà là chữ số La Mã tương ứng với số "5", xuất phát từ một quy tắc phân loại khác, có nghĩa là các sao thuộc dãy chính (tức là các sao tuổi nguyên tố).
Nhiệt độ bề mặt của Mặt Trời vào khoảng 5.537 độ C, trong khi đó nhiệt độ bên trong lõi của Mặt Trời lên đến khoảng 15 triệu độ C.

Có nhiều phương pháp khác nhau để ước tính nhiệt độ mặt trời , từ "tia nhiệt" không tồn tại đến Định luật làm mát Newton . Theo như kết quả tính toán, Mặt trời sẽ có thể đo từ hơn 1.000 độ đến vài triệu độ. ?
Để khuyến khích những nghiên cứu đáng tin cậy và chính xác, năm 1876, Viện Hàn lâm Khoa học Paris ở Pháp đã đặc biệt thiết lập một giải thưởng về tính toán nhiệt độ của mặt trời, nhưng rất tiếc là phương pháp này chưa thật chính xác. Dù giải thưởng đã được trao cho nhà vật lý người Pháp Jules Violle (1841 -1923). Nhưng phương pháp của ông thu được kết quả bằng phép tính rất "không đáng tin cậy" Mặt trời có nhiệt độ ở 1500-2500 ° C.

Joseph Stefan nhà vật lý, toán học, và nhà thơ gốc Slovenia của Đế quốc Áo
Cơ sở lý thuyết để tính nhiệt độ của mặt trời đã được nhà vật lý người Áo Joseph Stefan (Joseph Stefan, 1835-1893) đưa ra từ năm 1879 và 1884 từ dữ liệu thực nghiệm, và sau đó là đồng hương của ông là Ludwig Boltzmann (Ludwig Boltzmann, 1893) năm 1844. -1906) tiếp tục thực hiện các nghiên cứu có nguồn gốc từ nhiệt động lực học.

Ludwig Boltzmann
Hai nhà khoa học phát hiện ra rằng công suất bức xạ trên một đơn vị diện tích của vật đen (nghĩa là năng lượng bức xạ trong một giây) tỷ lệ với nhiệt độ tuyệt đối được nâng lên lũy thừa thứ tư. Định luật này ngày nay được gọi là định luật Stefan-Boltzmann, và hệ số tỷ lệ được gọi là hằng số Stefan-Boltzmann. Trong Hệ đơn vị Quốc tế, giá trị của hằng số Stefan-Boltzmann là
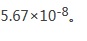
Mặc dù định luật Stefan-Boltzmann nhằm vào vật đen, nhưng hầu hết bức xạ sao tương đối gần với bức xạ vật đen, vì vậy định luật này cũng có thể áp dụng gần đúng cho bức xạ sao. Với định luật này, có một cơ sở lý thuyết để tính toán nhiệt độ bề mặt của mặt trời.
Phương pháp tính toán rất đơn giản: (theo thang nhiệt độ tuyệt đối) lũy thừa thứ tư của nhiệt độ bề mặt nhân với hằng số Stefan-Boltzmann là công suất bức xạ trên một mét vuông bề mặt của mặt trời, sau đó nhân với diện tích bề mặt của Mặt trời, nó là tổng bức xạ của mặt trời Công suất (nghĩa là tổng năng lượng bức xạ trong một giây), là độ chói của mặt trời của chúng ta.
Với phương pháp trên, Không khó để có được - nhiệt độ bề mặt của mặt trời (chính xác là nhiệt độ hiệu dụng của quang quyển ) vào khoảng 5800K (K là đơn vị nhiệt độ của thang nhiệt độ tuyệt đối, và 0 ° C trên thang độ C là khoảng 273K).
Ngoài phương pháp trên, các nhà khoa học còn có phương pháp nào ?
Trong phép tính trên, ngoài việc sử dụng định luật Stefan-Boltzmann, còn cần biết giá trị của hằng số Stefan-Boltzmann và độ chói của mặt trời. Nhưng trên thực tế, miễn là có mối quan hệ lũy thừa thứ tư được đưa ra bởi định luật Stefan-Boltzmann, ngay cả khi chúng ta không biết độ lớn của hằng số Stefan-Boltzmann, hoặc thậm chí độ chói của mặt trời, chúng ta vẫn có thể tính được nhiệt độ bề mặt của mặt trời.
Phương pháp này cũng rất đơn giản: chúng ta biết rằng nhiệt độ trung bình của bề mặt trái đất là khoảng 290K (tức là 17 ° C - đây là mức trung bình kép của vị trí và thời gian), nhưng một hành tinh có nhiệt độ như vậy cũng bức xạ năng lượng hướng ra bên ngoài, và năng lượng này cũng có thể được mô tả gần đúng bằng định luật Stefan-Boltzmann.
Vì không thể tự phát ra ánh sáng như mặt trời nên năng lượng trên bề mặt Trái đất chủ yếu đến từ ánh sáng mặt trời. Ngoài ánh sáng mặt trời, năng lượng nhận được trên bề mặt trái đất còn có sự đóng góp của bên trong trái đất. Tuy nhiên, công suất trung bình của cái sau chỉ là 0,06 W / m2, nhỏ hơn 1 / 10.000 năng lượng của ánh sáng mặt trời và có thể bị bỏ qua trong tính toán bằng phương pháp này.
Trái đất có thể duy trì nhiệt độ bề mặt hiện tại, có nghĩa là năng lượng mà nó tỏa ra về cơ bản bằng với năng lượng mà nó nhận được từ ánh sáng mặt trời. Sử dụng mối quan hệ này, chúng ta có thể tính toán nhiệt độ bề mặt của mặt trời.
Bạn thấy hằng số Stefan-Boltzmann sẽ tự động bị loại bỏ trong quá trình tính toán, và kết quả tính được là khoảng 6000K, tuy không chính xác như phương pháp trước nhưng cũng không khác nhiều.
Điều thú vị của phương pháp này là sử dụng nhiệt độ của hành tinh để suy ra nhiệt độ của ngôi sao. Nhưng điều thú vị hơn là, chúng ta cũng có thể suy ra nhiệt độ của các hành tinh ở một khoảng cách nhất định so với nhiệt độ của ngôi sao. Phương pháp này thường được các nhà thiên văn học sử dụng để ước tính vị trí và chiều rộng của vùng có thể sinh sống xung quanh một ngôi sao có khả năng tồn tại sự sống.
Tất nhiên, phương pháp tính toán này có những hạn chế lớn, ví dụ, nó đòi hỏi sự tồn tại của những thứ như nước và khí quyển trên hành tinh có thể làm cho nhiệt độ đồng nhất, và cũng yêu cầu bầu khí quyển không chứa nhiều khí gây hiệu ứng nhà kính ví dụ như khí quyển của sao Kim.
Ngay sau khi định luật Stefan-Boltzmann ra đời, nhà vật lý người Đức Wilhelm Wien (1864-1928) đã sử dụng nhiệt động lực học để chứng minh một định luật gọi là định luật chuyển vị Wien. (Wien‘s displacement law)

Wilhelm Carl Werner Otto Fritz Franz Wien
Định luật này cho thấy rằng nhiệt độ bề mặt của vật thể càng cao thì sự phân bố quang phổ càng bị dịch chuyển theo hướng sóng ngắn và màu sắc bị chuyển sang hướng xanh lam.
Áp dụng định luật này, các nhà thiên văn học đã phân loại các ngôi sao thành bảy loại theo đặc điểm quang phổ của chúng, được ký hiệu lần lượt là O, B, A, F, G, K và M.

Các thiên thể màu vàng như mặt trời thuộc loại G và có nhiệt độ bề mặt từ 5200 đến 6000K. Trong mười loại phụ được chia theo thứ tự nhiệt độ từ cao đến thấp, được biểu thị bằng các chữ số Ả Rập từ 0 đến 9, 0 có nghĩa là nhiệt độ cao nhất và 9 có nghĩa là nhiệt độ thấp nhất.
Loại quang phổ của mặt trời là G2, được coi là loại có nhiệt độ cao hơn trong số loại G. Trong một số tài liệu, quang phổ của mặt trời được đánh dấu là G2V, khiến nó có màu trắng, và thường có màu vàng khi nhìn từ bề mặt Trái Đất bởi sự tán xạ khí quyển . Trong đó "V" không phải là chữ cái tiếng Anh "V", mà là chữ số La Mã tương ứng với số "5", xuất phát từ một quy tắc phân loại khác, có nghĩa là các sao thuộc dãy chính (tức là các sao tuổi nguyên tố).
BÀI MỚI ĐANG THẢO LUẬN

