Vn-Z.vn Ngày 21 tháng 08 năm 2022, Trong toán học có nhiều bí ẩn kéo dài hàng thập kỷ vẫn chưa tìm được ra đáp án. Liên quan đến phương trình Pell cổ điển trong lý thuyết số cơ bản: x²-dy² = 1. (Ở đây d là một số nguyên và x và y cũng là các nghiệm nguyên.)
Trước đây, các nghiệm nguyên cho phương trình Pell cổ điển đã được chứng minh như sau:
Khi d≤0 hoặc d là một số chính phương lớn hơn 0 thì phương trình có nghiệm duy nhất: x = ± 1, y = 0; khi d> 0 và không phải là số bình phương hoàn hảo thì phương trình không có dãy số nguyên dương.
Nhưng các nhà toán học nói chung không dừng lại ở kết quả đó. Có ai đó đã đề xuất thay đổi số 1 ở bên phải của phương trình Pell thành -1, và gọi phương trình mới này là phương trình Pell âm (Phương trình Pell loại II), ngay lập tức nó trở nên phức tạp hơn nhiều đối với phần tìm nghiệm nguyên.
Quay lại năm 1993, khi nhà toán học Peter Stevenhargen đưa ra công thức và câu trả lời chính xác cho các nghiệm nguyên của phương trình Pell âm. Sau 30 năm sau , phỏng đoán về phương trình này đã được đề xuất nhưng cộng đồng toán học đã không thể chứng minh tính đúng đắn của nó.
Nhưng bây giờ, Carlo Pagano của Đại học Concordia và Peter Koymans của Đại học Michigan cuối cùng đã đưa ra một "giải pháp chính xác" cho phương trình Pell âm.
Giáo sư Hendrik Lenstra, người cố vấn của Pagano, thậm chí còn bình luận về điều này: Kết quả này mở ra một chương mới trong một nhánh của lý thuyết số.
Mời anh em Vn-Z cùng tìm hiểu về phương trình này nhé
Trước khi giới thiệu phương trình Pell âm, đầu tiên chúng ta hãy tìm hiểu xem phương trình Pell cổ điển bắt nguồn từ đâu. Thực tế, phương trình Pell không liên quan gì đến Pell cả. Lý thuyết này lần đầu tiên được nghiên cứu bởi Pierre de Fermat, và giải pháp đã được đưa ra bởi Joseph-Louis Lagrange, nhưng sau đó nó được đề xuất bởi Leonhard Euler vì ông bị nhớ nhầm là Pell. Cái tên Pell được gọi cho phương tình này như một cách tình cờ.
Dạng cụ thể của nó là: x²-dy² = 1 Khi d là số nguyên dương và không phải là hình vuông hoàn hảo thì phương trình có vô số nghiệm.
Ví dụ này được cụ thể trong Bài toán đàn gia súc Archimedes , đây là bài toán giải phương trình Diophantine kinh điển trong lịch sử toán học. Bài toán yêu cầu tính số bò trong đàn gia súc của Thần Mặt Trời. Bài toán được Gothold Ephraim Lessing phát hiện ra trong một văn bản Hy Lạp cổ, dưới dạng một bài thơ 44 dòng.
Thần mặt trời nuôi một đàn bò, đàn bò này có đực và cái, phân thành bốn màu:Trắng sữa, đen, đốm và vàng.. Với một loạt các điều kiện, tổng số bò có bao nhiêu? Có bao nhiêu con bò với nhiều màu sắc khác nhau? Câu hỏi này luôn thu hút sự quan tâm của nhiều nhà toán học. Cuối cùng, sau một loạt các phép tính, để giải bài toán này người ta dẫn đến giải một phương trình Pell:
x²-4729494*y²=1
Bài toán này đã được giải quyết hoàn toàn bởi Lenstra vào năm 2000, Lenstra đã đưa ra tất cả các giải pháp cho vấn đề trong bài toán Archimedes:
Đáp số: số lượng gia súc của Thần Mặt Trời xấp xỉ 7.76 × 10 206544
Không giống như phương trình Pell, nghiệm nguyên cho phương trình Pell âm phức tạp hơn nhiều.
Phương trình Pell âm
Phương trình Pell âm có thể được biểu diễn dưới dạng: x²-dy² = -1 Rõ ràng, khi d≤0 và d là bình phương lớn hơn 1, phương trình không có nghiệm nguyên.
Ngoài ra, sự phức tạp của các nghiệm nguyên đối với phương trình Pell âm còn thể hiện ở chỗ nhiều giá trị của d trong phương trình Pell âm không có nghiệm nguyên. Theo các quy tắc đã biết, d không thể là bội số của 3, 7, 11, 15, v.v. Nhưng ngoài các giá trị này, không phải tất cả các giá trị khác của d nhất thiết phải có nghiệm nguyên.
Ví dụ, khi d = 3, x²–3 * y² = -1, bất kể dọc theo trục số bao xa, lời giải sẽ không bao giờ được tìm thấy. Nhưng trên thực tế, sau khi loại trừ bội số của 3, 7, 11, 15, thay vì lấy các giá trị d khác, phương trình Pell âm phải có nghiệm nguyên. Với giá trị của d, nghiệm cơ bản của phương trình Pell âm cần phải được tìm thấy trước tiên.
Có thể thu được một giải pháp chung cho phương trình Pell âm bằng công thức sau:
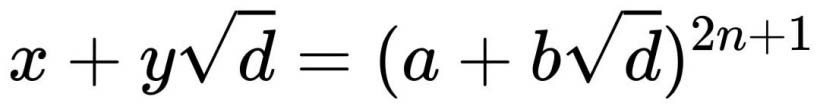
Với n là bất kỳ số nguyên dương nào; a và b là nghiệm cơ bản của phương trình Pell âm, có các phương trình sau:
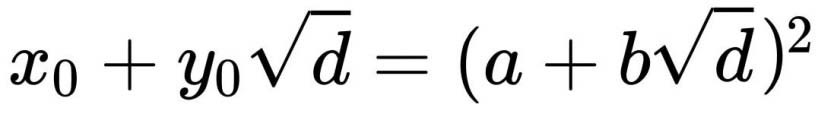
x0 và y0 là các nghiệm cơ bản của phương trình Pell cổ điển.
Bạn đọc có thể tham khảo thêm các bài viết dưới đây
www.quantamagazine.org
vi.wikipedia.org
Trước đây, các nghiệm nguyên cho phương trình Pell cổ điển đã được chứng minh như sau:
Khi d≤0 hoặc d là một số chính phương lớn hơn 0 thì phương trình có nghiệm duy nhất: x = ± 1, y = 0; khi d> 0 và không phải là số bình phương hoàn hảo thì phương trình không có dãy số nguyên dương.
Nhưng các nhà toán học nói chung không dừng lại ở kết quả đó. Có ai đó đã đề xuất thay đổi số 1 ở bên phải của phương trình Pell thành -1, và gọi phương trình mới này là phương trình Pell âm (Phương trình Pell loại II), ngay lập tức nó trở nên phức tạp hơn nhiều đối với phần tìm nghiệm nguyên.
Nhưng bây giờ, Carlo Pagano của Đại học Concordia và Peter Koymans của Đại học Michigan cuối cùng đã đưa ra một "giải pháp chính xác" cho phương trình Pell âm.
Giáo sư Hendrik Lenstra, người cố vấn của Pagano, thậm chí còn bình luận về điều này: Kết quả này mở ra một chương mới trong một nhánh của lý thuyết số.
Mời anh em Vn-Z cùng tìm hiểu về phương trình này nhé
Trước khi giới thiệu phương trình Pell âm, đầu tiên chúng ta hãy tìm hiểu xem phương trình Pell cổ điển bắt nguồn từ đâu. Thực tế, phương trình Pell không liên quan gì đến Pell cả. Lý thuyết này lần đầu tiên được nghiên cứu bởi Pierre de Fermat, và giải pháp đã được đưa ra bởi Joseph-Louis Lagrange, nhưng sau đó nó được đề xuất bởi Leonhard Euler vì ông bị nhớ nhầm là Pell. Cái tên Pell được gọi cho phương tình này như một cách tình cờ.
Dạng cụ thể của nó là: x²-dy² = 1 Khi d là số nguyên dương và không phải là hình vuông hoàn hảo thì phương trình có vô số nghiệm.
Ví dụ này được cụ thể trong Bài toán đàn gia súc Archimedes , đây là bài toán giải phương trình Diophantine kinh điển trong lịch sử toán học. Bài toán yêu cầu tính số bò trong đàn gia súc của Thần Mặt Trời. Bài toán được Gothold Ephraim Lessing phát hiện ra trong một văn bản Hy Lạp cổ, dưới dạng một bài thơ 44 dòng.
Thần mặt trời nuôi một đàn bò, đàn bò này có đực và cái, phân thành bốn màu:Trắng sữa, đen, đốm và vàng.. Với một loạt các điều kiện, tổng số bò có bao nhiêu? Có bao nhiêu con bò với nhiều màu sắc khác nhau? Câu hỏi này luôn thu hút sự quan tâm của nhiều nhà toán học. Cuối cùng, sau một loạt các phép tính, để giải bài toán này người ta dẫn đến giải một phương trình Pell:
x²-4729494*y²=1
Bài toán này đã được giải quyết hoàn toàn bởi Lenstra vào năm 2000, Lenstra đã đưa ra tất cả các giải pháp cho vấn đề trong bài toán Archimedes:
Đáp số: số lượng gia súc của Thần Mặt Trời xấp xỉ 7.76 × 10 206544
Không giống như phương trình Pell, nghiệm nguyên cho phương trình Pell âm phức tạp hơn nhiều.
Phương trình Pell âm
Phương trình Pell âm có thể được biểu diễn dưới dạng: x²-dy² = -1 Rõ ràng, khi d≤0 và d là bình phương lớn hơn 1, phương trình không có nghiệm nguyên.
Ngoài ra, sự phức tạp của các nghiệm nguyên đối với phương trình Pell âm còn thể hiện ở chỗ nhiều giá trị của d trong phương trình Pell âm không có nghiệm nguyên. Theo các quy tắc đã biết, d không thể là bội số của 3, 7, 11, 15, v.v. Nhưng ngoài các giá trị này, không phải tất cả các giá trị khác của d nhất thiết phải có nghiệm nguyên.
Ví dụ, khi d = 3, x²–3 * y² = -1, bất kể dọc theo trục số bao xa, lời giải sẽ không bao giờ được tìm thấy. Nhưng trên thực tế, sau khi loại trừ bội số của 3, 7, 11, 15, thay vì lấy các giá trị d khác, phương trình Pell âm phải có nghiệm nguyên. Với giá trị của d, nghiệm cơ bản của phương trình Pell âm cần phải được tìm thấy trước tiên.
Có thể thu được một giải pháp chung cho phương trình Pell âm bằng công thức sau:
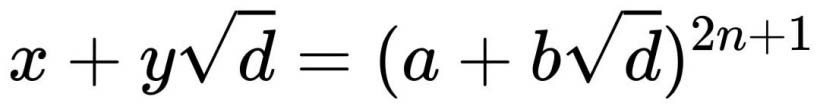
Với n là bất kỳ số nguyên dương nào; a và b là nghiệm cơ bản của phương trình Pell âm, có các phương trình sau:
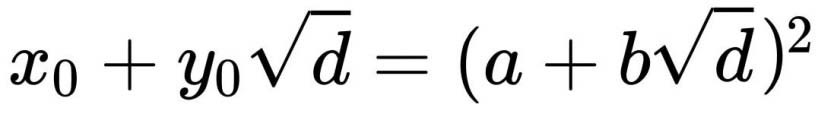
x0 và y0 là các nghiệm cơ bản của phương trình Pell cổ điển.
Bạn đọc có thể tham khảo thêm các bài viết dưới đây
Ancient Equations Offer New Look at Number Groups | Quanta Magazine
Ever since Archimedes, mathematicians have been fascinated by equations that involve a difference between squares. Now two mathematicians have proven how often these equations have solutions, concluding a decades-old quest.
